Многие люди не начинают пользоваться криптовалютой биткоин отчасти потому, что для них она остается чем-то загадочным и непонятным, и переворачивает с ног на голову привычное представление о деньгах и собственности. Традиционно люди представляют собственность, как нечто физическое, что находится лично у человека или его представителя. Однако сложно подогнать биткоин под этот стереотип, так как криптовалюта существует лишь в блокчейн, и быть владельцем биткоин означает лишь возможность передать BTC кому-либо и зафиксировать этот факт в блокчейн. Для того, чтобы разобраться, чем именно это интересно и почему стоит предпочесть биткоин другим видам денег и платежей, нужно немного углубиться в термины и математику.
Одним из ключевых понятий криптовалюты биткоин является ключ ECDSA, аббревиатура от Алгоритма Цифровой Подписи с Эллиптическими Кривыми. С его помощью возможно «подписать» данные таким образом, что третьи лица могут легко проверить подлинность подписи, но подделать ее невозможно. Оставить подпись сможет только сам ее автор. В биткоинах «данные», которые подписываются — это ни что иное, как транзакция, которая и передает право собственности на биткойны от одного пользователя другому. Для проверки подписи в алгоритме существуют две процедуры, состоящие из нескольких арифметических операций.
Для того, чтобы подписать данные, алгоритм ECDSA использует эллиптические кривые и конечные поля. Подробнее о них:
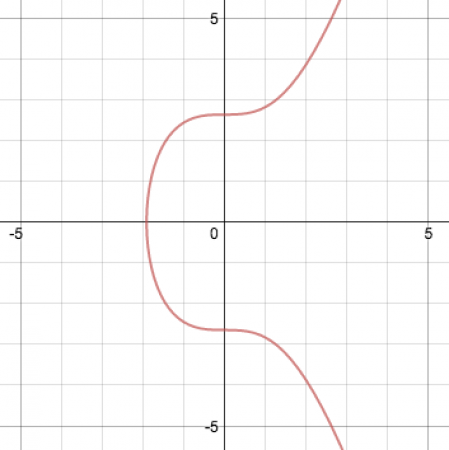
Эллиптическая кривая, с точки зрения математики, представляет собой уравнение y² = x³ + ах + b
Для а = 0 и b = 7 (а это именно та версия, которую использует Биткойн), эта кривая выглядит так:
Эллиптические кривые имеют некоторые полезные свойства. Например, не-вертикальная прямая, пересекающая кривую в двух точках, всегда будет пересекать ее и в третьей точке, лежащей на кривой. Другим свойством является то, что если не-вертикальная прямая является касательной к кривой в одной из точек, то она обязательно пересекает кривую еще ровно в одной точке.
Мы можем использовать эти свойства, чтобы определить две операции над точками, составляющими кривую: сложение точек и удвоение.
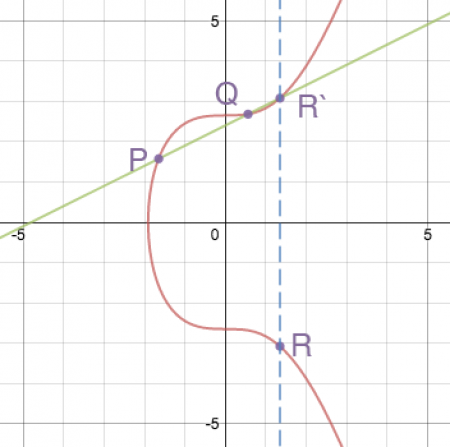
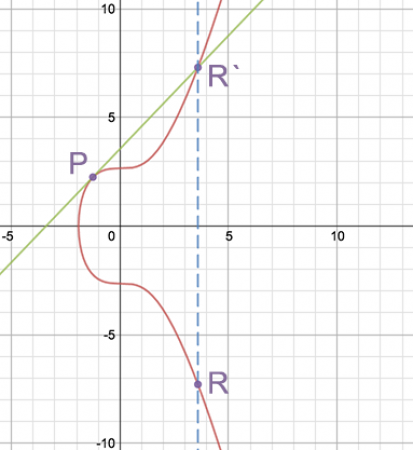
Для сложения точек, P + Q = R, мы проводим через точки P и Q прямую, которая, по свойствам эллиптических кривых, пересекает кривую в некоторой третьей точке R‘. Затем мы находим точку на кривой, симметричную точке R‘ относительно оси X. Именно эта точка R и будет считаться суммой P и Q. Это легче всего понять это, глядя на следующую схему:
Эллиптические кривые имеют некоторые полезные свойства. Например, не-вертикальная прямая, пересекающая кривую в двух точках, всегда будет пересекать ее и в третьей точке, лежащей на кривой. Другим свойством является то, что если не-вертикальная прямая является касательной к кривой в одной из точек, то она обязательно пересекает кривую еще ровно в одной точке.
Мы можем использовать эти свойства, чтобы определить две операции над точками, составляющими кривую: сложение точек и удвоение.
Для сложения точек, P + Q = R, мы проводим через точки P и Q прямую, которая, по свойствам эллиптических кривых, пересекает кривую в некоторой третьей точке R‘. Затем мы находим точку на кривой, симметричную точке R‘ относительно оси X. Именно эта точка R и будет считаться суммой P и Q. Это легче всего понять это, глядя на следующую схему:
Это все хорошо, но как бы нам сложить точку саму с собой? Для этого, определяется операция удвоения точки, P + P = R. При удвоении, мы проводим прямую, касательную к данной эллиптической кривой в точке P, которая, согласно свойствам кривой, должна пересекать ее еще в одной точке R‘. Точка R, симметричная R‘относительно оси X, и будет считаться точкой удвоения P. На графике это выглядит следующим образом:
Это все хорошо, но как бы нам сложить точку саму с собой? Для этого, определяется операция удвоения точки, P + P = R. При удвоении, мы проводим прямую, касательную к данной эллиптической кривой в точке P, которая, согласно свойствам кривой, должна пересекать ее еще в одной точке R‘. Точка R, симметричная R‘относительно оси X, и будет считаться точкой удвоения P. На графике это выглядит следующим образом:
Эти две операции можно использовать, чтобы определить операцию скалярного умножения, R = a P, определяемую как добавление точки Р самой к себе a раз. Например:
R = 7P
R = P + (P + (P + (P + (P + (P + P)))))
Процесс скалярного умножения, как правило, можно упростить, используя комбинацию сложения и удвоения точек. Например:
R = 7P
R = P + 6P
R = P + 2 (3P)
R = P + 2 (Р + 2P)
Здесь операция 7P была разбита на два этапа удвоения точек и два сложения точек — в итоге, вместо 7 операций нужно произвести всего четыре.
Собственно, теперь вы знаете об эллиптических кривых все, что о них стоит знать.
Конечные поля
Теперь поговорим немного о конечных полях. Конечное поле, в контексте ECDSA, можно рассматривать как заданный диапазон положительных чисел. Любые операции должны осуществляться в рамках этого диапазона — если же результат операции выходит за пределы этого диапазона, мы не расстраиваемся, а просто по окончании диапазона возвращаемся к его началу и продолжаем считать как ни в чем ни бывало. Таким образом, результат все равно окажется внутри нашего диапазона, как бы он ни хотел из него выбраться.
Самый простой способ проиллюстрировать это — расчет операции «остаток от целочисленного деления», или оператор модуло (MOD). Например, 9/7 дает 1 с остатком 2:
9 MOD 7 = 2
Здесь мы имеем конечное поле от 0 до 6, и все операции по модулю 7, над каким бы числом они не осуществлялись, дадут результат попадающий в этот диапазон.
Скрещиваем кривые с полями
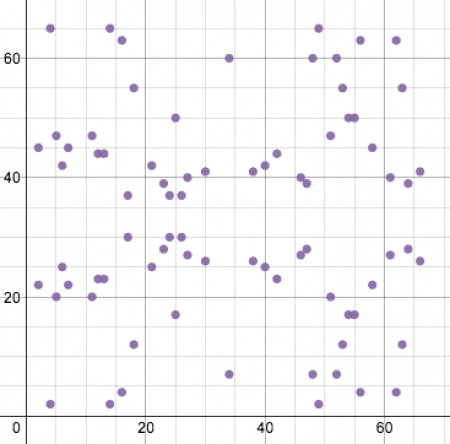
ECDSA использует не просто эллиптические кривые, а эллиптические кривые в контексте конечного поля, что значительно меняет их внешний вид. Причем меняет его так, что теперь эти самые кривые даже родная мама не узнает. Допустим, та же самая красивая эллиптическая кривая Биткойна, y² = x³ + 7, которая изображена выше, но только определенная на конечном поле по модулю 67, выглядит как такая вот странная крякозябра:
Эти две операции можно использовать, чтобы определить операцию скалярного умножения, R = a P, определяемую как добавление точки Р самой к себе a раз. Например:
R = 7P
R = P + (P + (P + (P + (P + (P + P)))))
Процесс скалярного умножения, как правило, можно упростить, используя комбинацию сложения и удвоения точек. Например:
R = 7P
R = P + 6P
R = P + 2 (3P)
R = P + 2 (Р + 2P)
Собственно, теперь вы знаете об эллиптических кривых все, что о них стоит знать.
Конечные поля
Теперь поговорим немного о конечных полях. Конечное поле, в контексте ECDSA, можно рассматривать как заданный диапазон положительных чисел. Любые операции должны осуществляться в рамках этого диапазона — если же результат операции выходит за пределы этого диапазона, мы не расстраиваемся, а просто по окончании диапазона возвращаемся к его началу и продолжаем считать как ни в чем ни бывало. Таким образом, результат все равно окажется внутри нашего диапазона, как бы он ни хотел из него выбраться.
Самый простой способ проиллюстрировать это — расчет операции «остаток от целочисленного деления», или оператор модуло (MOD). Например, 9/7 дает 1 с остатком 2:
9 MOD 7 = 2
Здесь мы имеем конечное поле от 0 до 6, и все операции по модулю 7, над каким бы числом они не осуществлялись, дадут результат попадающий в этот диапазон.
Скрещиваем кривые с полями
ECDSA использует не просто эллиптические кривые, а эллиптические кривые в контексте конечного поля, что значительно меняет их внешний вид. Причем меняет его так, что теперь эти самые кривые даже родная мама не узнает. Допустим, та же самая красивая эллиптическая кривая Биткойна, y² = x³ + 7, которая изображена выше, но только определенная на конечном поле по модулю 67, выглядит как такая вот странная крякозябра:
Однако, заметим в ее оправдание, что хотя она и стала неузнаваемой для непосвященных, лежащие в основе этой «кривой» уравнения или ее особые свойства ничуть не изменились. Просто теперь это множество точек, в которых все х и у значения представляют собой целые между 0 и 66 Отметим также, что «кривая» по-прежнему сохраняет свою горизонтальную симметрию.
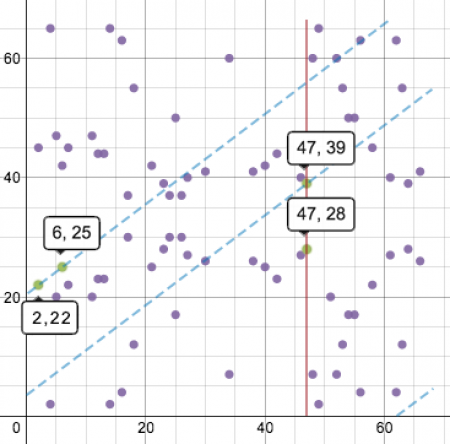
Правда, процесс операций над точками: сложения и удвоения — сейчас будет немного отличаться визуально. «Прямые линии», нарисованные на этом графике, теперь будут оборачиваться «вокруг поля», как только они достигнут магического барьера 67, как в древней аркадной игре «Asteroids», и продолжаться с другого его конца, сохраняя прежний наклон, но со сдвигом. Поэтому, сложение точек (2, 22) и (6, 25) в данном дискретном варианте выглядит следующим образом:
Однако, заметим в ее оправдание, что хотя она и стала неузнаваемой для непосвященных, лежащие в основе этой «кривой» уравнения или ее особые свойства ничуть не изменились. Просто теперь это множество точек, в которых все х и у значения представляют собой целые между 0 и 66 Отметим также, что «кривая» по-прежнему сохраняет свою горизонтальную симметрию.
Правда, процесс операций над точками: сложения и удвоения — сейчас будет немного отличаться визуально. «Прямые линии», нарисованные на этом графике, теперь будут оборачиваться «вокруг поля», как только они достигнут магического барьера 67, как в древней аркадной игре «Asteroids», и продолжаться с другого его конца, сохраняя прежний наклон, но со сдвигом. Поэтому, сложение точек (2, 22) и (6, 25) в данном дискретном варианте выглядит следующим образом:
«Оборачивающаяся прямая», проходящая через эти две точки, в итоге уперлась в третью точку (47, 39), а симметричная ей «относительно оси X» будет (47, 28). Вот эта-то точка и станет результатом нашей операции.
Применим свою математическую мудрость к криптографии
Чтобы использовать ECDSA, такой протокол как Биткойн должен зафиксировать набор параметров для эллиптической кривой и ее конечного поля, чтобы эти параметры знали и применяли все пользователи протокола. Иначе, каждый будет решать свои собственные уравнения, которые не будут сходиться друг с другом, и они никогда ни о чем не договорятся.
Эти зафиксированные параметры включают в себя уравнение кривой, значение модуля поля, и базовую точку, которая лежит на кривой. Последним параметром является порядок базовой точки, который в графическом виде можно представить себе как количество раз, которое базовая точка может быть прибавлена к себе до тех пор, пока ее касательная кривая не станет вертикальной. Этот параметр подбирается таким образом, чтобы он являлся очень большим простым числом.
Для всех этих параметров, Биткойн использует очень-очень большие (ну просто офигенно невообразимо огромные) числа. Это важно. На самом деле, все практические применения ECDSA используют огромные числа. Ведь безопасность этого алгоритма опирается на то, что эти значения слишком большие чтобы подобрать что-то простым перебором или «брутфорсом».
В случае Биткойна, эти значения таковы (запись чисел дана не в десятичном, а в более компактном шестнадцатеричном виде, привычном программистам):
Уравнение эллиптической кривой: y² = x³ + 7
Простой модуль = 2256 — 232 — 29 — 28 — 27 — 26 — 24 — 1 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
Базовая точка = 04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
Порядок = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141
Кто выбрал эти цифры, и почему? Большое количество исследований, и изрядная интрига, всегда окружает выбор соответствующих параметров. В конце концов, большое и, казалось бы, случайное число может скрывать в себе какую-нибудь «заднюю дверцу» для упрощения вычислений, которая может быть доступна только посвященным. Если вкратце, данная конкретная реализация ECDSA известна как secp256k1 и является частью семейства стандартов, предлагаемых для использования в криптографии.
Вооружившись всеми этими базовыми знаниями, в следующей статье мы будем готовы применить эту математику к Биткойну и выяснить, наконец, что же там происходит в недрах нашего биткойн-клиента, когда мы нажимаем на кнопку «Оплатить». Ну, а пока вы ждете второй части, можете слегка освежить свои знания относительно анатомии биткойн-адресов и транзакций. А если вы разработчик, то можно полюбопытствовать, что же там происходит внутри этого таинственного API биткойн-протокола.
«Оборачивающаяся прямая», проходящая через эти две точки, в итоге уперлась в третью точку (47, 39), а симметричная ей «относительно оси X» будет (47, 28). Вот эта-то точка и станет результатом нашей операции.
Применим свою математическую мудрость к криптографии
Чтобы использовать ECDSA, такой протокол как Биткойн должен зафиксировать набор параметров для эллиптической кривой и ее конечного поля, чтобы эти параметры знали и применяли все пользователи протокола. Иначе, каждый будет решать свои собственные уравнения, которые не будут сходиться друг с другом, и они никогда ни о чем не договорятся.
Эти зафиксированные параметры включают в себя уравнение кривой, значение модуля поля, и базовую точку, которая лежит на кривой. Последним параметром является порядок базовой точки, который в графическом виде можно представить себе как количество раз, которое базовая точка может быть прибавлена к себе до тех пор, пока ее касательная кривая не станет вертикальной. Этот параметр подбирается таким образом, чтобы он являлся очень большим простым числом.
Для всех этих параметров, Биткойн использует очень-очень большие (ну просто офигенно невообразимо огромные) числа. Это важно. На самом деле, все практические применения ECDSA используют огромные числа. Ведь безопасность этого алгоритма опирается на то, что эти значения слишком большие чтобы подобрать что-то простым перебором или «брутфорсом».
В случае Биткойна, эти значения таковы (запись чисел дана не в десятичном, а в более компактном шестнадцатеричном виде, привычном программистам):
Уравнение эллиптической кривой: y² = x³ + 7
Простой модуль = 2256 — 232 — 29 — 28 — 27 — 26 — 24 — 1 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
Базовая точка = 04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
Порядок = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141
Кто выбрал эти цифры, и почему? Большое количество исследований, и изрядная интрига, всегда окружает выбор соответствующих параметров. В конце концов, большое и, казалось бы, случайное число может скрывать в себе какую-нибудь «заднюю дверцу» для упрощения вычислений, которая может быть доступна только посвященным. Если вкратце, данная конкретная реализация ECDSA известна как secp256k1 и является частью семейства стандартов, предлагаемых для использования в криптографии.
Вооружившись всеми этими базовыми знаниями, в следующей статье мы будем готовы применить эту математику к Биткойну и выяснить, наконец, что же там происходит в недрах нашего биткойн-клиента, когда мы нажимаем на кнопку «Оплатить». Ну, а пока вы ждете второй части, можете слегка освежить свои знания относительно анатомии биткойн-адресов и транзакций. А если вы разработчик, то можно полюбопытствовать, что же там происходит внутри этого таинственного API биткойн-протокола.
Войти через Google
Сортировка:
Сортировать